#2 Determine the period of the function y = 3cos π/4x
#3 The terminal arm of angle θ in standard position intersects the unit circle at the point (m , n) . Which expression represents cotθ ?
#4 If the graph of the function shown below has the equation y = a cos b(x-c) + d, determine the value of d.
#5 Determine an equation of an asymptote of y = sec 3x .
#9 Determine the domain of y = log (x+1)
#10 Determine an equivalent expression
#12 As an iceberg melts during the summer, it loses 3% of its mass every 5 days. This iceberg reduces to 40% of its original mass after t days. Which equation could be used to determine the value of t ?
#13 Solve: log₂(log₉x)=-1
#15 Determine the number of pathways from point A to point B if only moves to the right and down are permitted.
#16 Which equation represents the graph of y = f (x) after it is vertically compressed by a factor of 1/2 and then translated 2 units to the left?
#17 Determine the inverse of the function f (x) = 4x +1 /3x .
#18 The y-intercept of the function y = f (x) is 5. Determine the y-intercept of y = -f (x) + 3 .
#19 The graph of the function y = f (x) is shown below.
#20 If the point (10, 6 ) is on the graph of y = f (x), what point must be on the graph of y = f (-2x-4) ?
#21 The graph of y = f (x) is shown on the left. Determine an equation of the function graphed on the right.
#22 Solve 2cos x = 2x , where -π≤x≤π
#23 The height above the ground, h metres, of a person on a Ferris wheel at time t seconds, is given by the formula h (t) = -20 cos 2π/40 t + 23 , where t≥0 . Determine the earliest time at which the person will be 15 m above the ground.
#24 A circle has a radius of 18 cm. If the length of arc AB is 21π cm, as shown in the diagram, determine the measure of the central angle θ in degrees.
#25 Determine the restrictions for
#26 Determine the common ratio of the geometric sequence
#27 Use the following information to answer questions 27 and 28. Sam gave his nephew, Norman, $1 on his 1st birthday, $2 on his 2nd birthday, $4 on his 3rd birthday, and so on. That is, on each subsequent birthday, Sam gave Norman double the previous year’s amount. How much money did Sam give Norman on his 15th birthday?
#28 In total, how much money did Sam give Norman up to and including his 21st birthday?
#30 In a geometric sequence, t 4 = 108 and t 6 = 243. Determine a possible first term
#31 If x – 2 , x + 4, 5x + 2 are three consecutive terms in a geometric sequence, determine the numerical value(s) of the common ratio(s).
#32 Change to logarithmic form a3 = b
#34 Determine the magnitude of an earthquake that is half as intense as an earthquake of magnitude 8.0 on the Richter scale.
#35 A license plate consists of 3 letters followed by 3 digits. The letters I, O, Q, U, Y and Z are not used. If repetitions of letters and digits are allowed, determine the total number of possible license plates (e.g. ABB603).
#36 Determine the number of different arrangements of all the letters in the word APPLESEED.
#37 In a standard deck of 52 cards, how many different 5-card hands are there that contain at most 2 face cards?
#38 In the expansion of (a2 – b)4, determine the middle term.
#39 In how many different ways can a family of 5 people (2 parents and 3 children) sit in a row if a parent must sit on each end of the row?
#40 Consider the following 2 events: Event A: A fair coin is tossed and shows tails. Event B: A fair 6-sided die is rolled and shows a number greater than 2. Determine P A and B ( ).
#41 The diagram below represents a sample space of 11 equally likely outcomes. Determine P(A) .
#42 Two hockey players, Tom and Jerry, each shoot a penalty shot at a goal. Tom has a 1/2 chance of scoring the goal and Jerry has a 2/5 chance of scoring the goal. Assuming independence, what is the probability that at least one of them will score the goal?
#43 A 3-card hand is dealt from a standard deck of 52 cards. What is the probability that the hand will contain exactly one queen?
#44 A fair coin is tossed 30 times. What is the probability that the coin will show heads fewer than 17 times?
 B
B  C
C 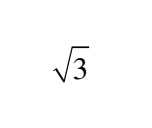 D
D 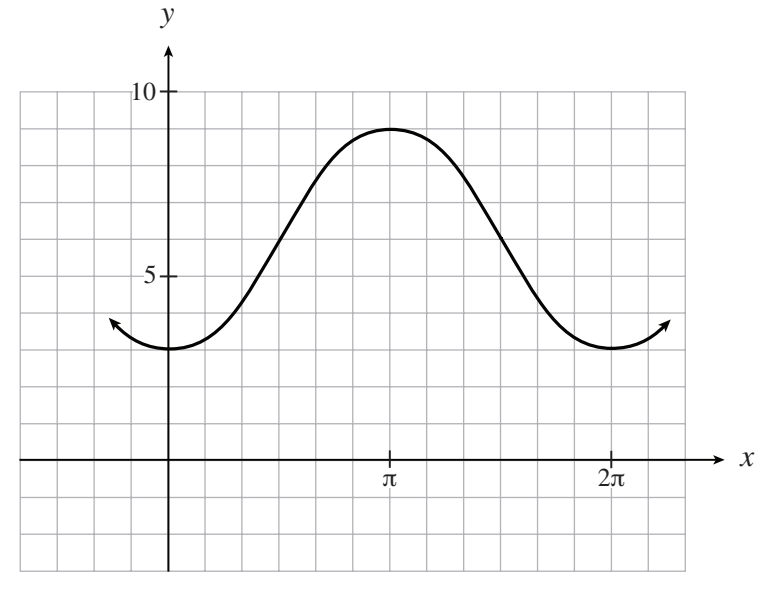
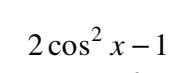 A
A 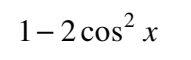 B
B  C
C 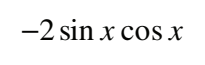 D
D 
 A
A 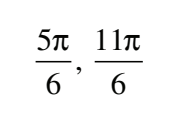 B
B 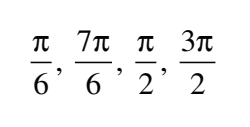 C
C 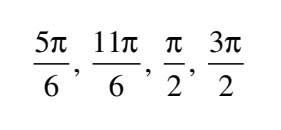 D
D 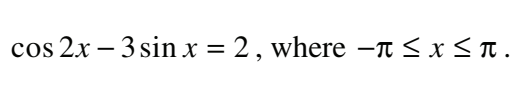
 A
A 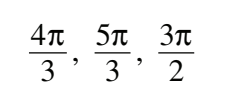 B
B 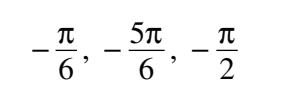 C
C 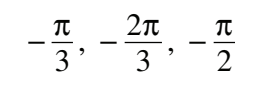 D
D 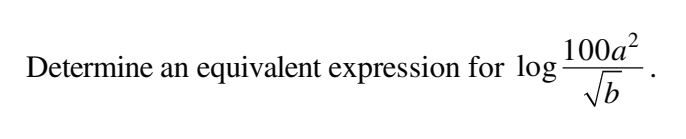
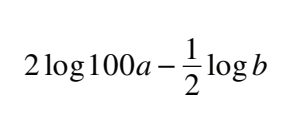 A
A 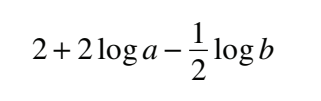 B
B 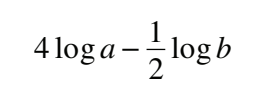 C
C 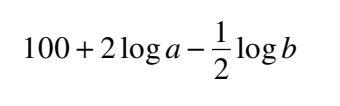 D
D 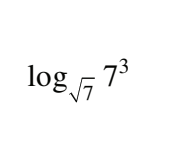
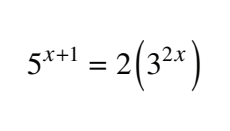
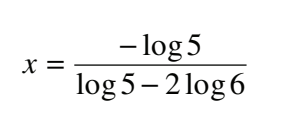 x = -log5/log5-2log6
x = -log5/log5-2log6  x=log2-log5/1-2log3
x=log2-log5/1-2log3  x=log2-log5/log5-2log3
x=log2-log5/log5-2log3 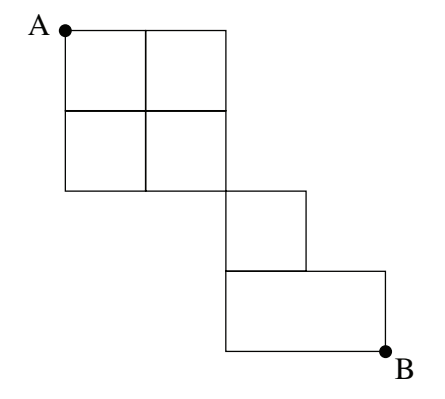
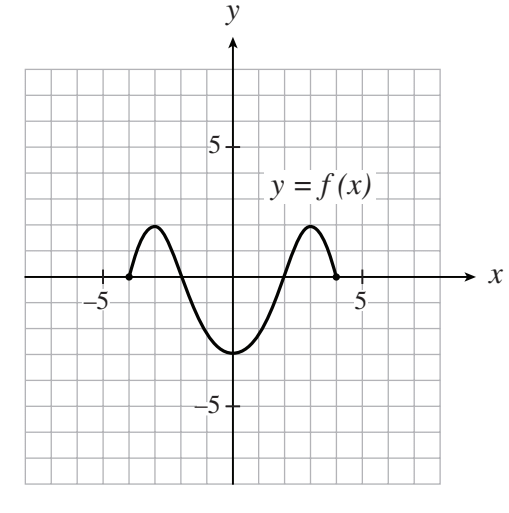
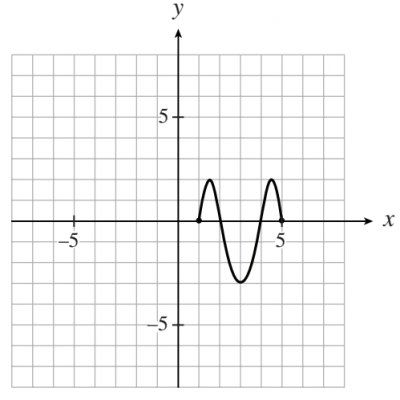 A
A 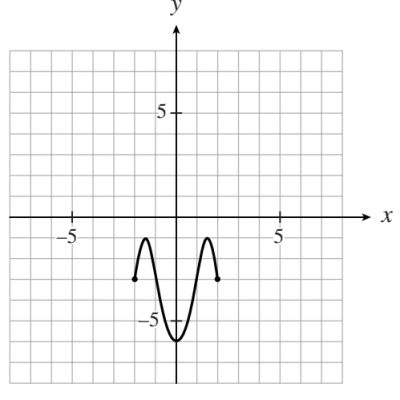 B
B 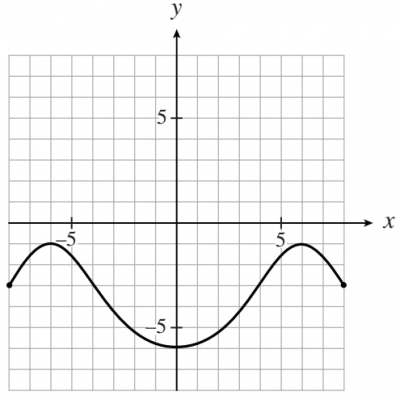 C
C 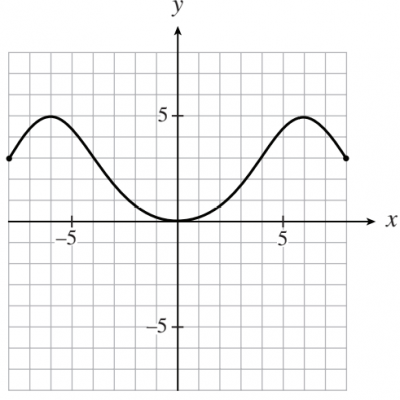 D
D 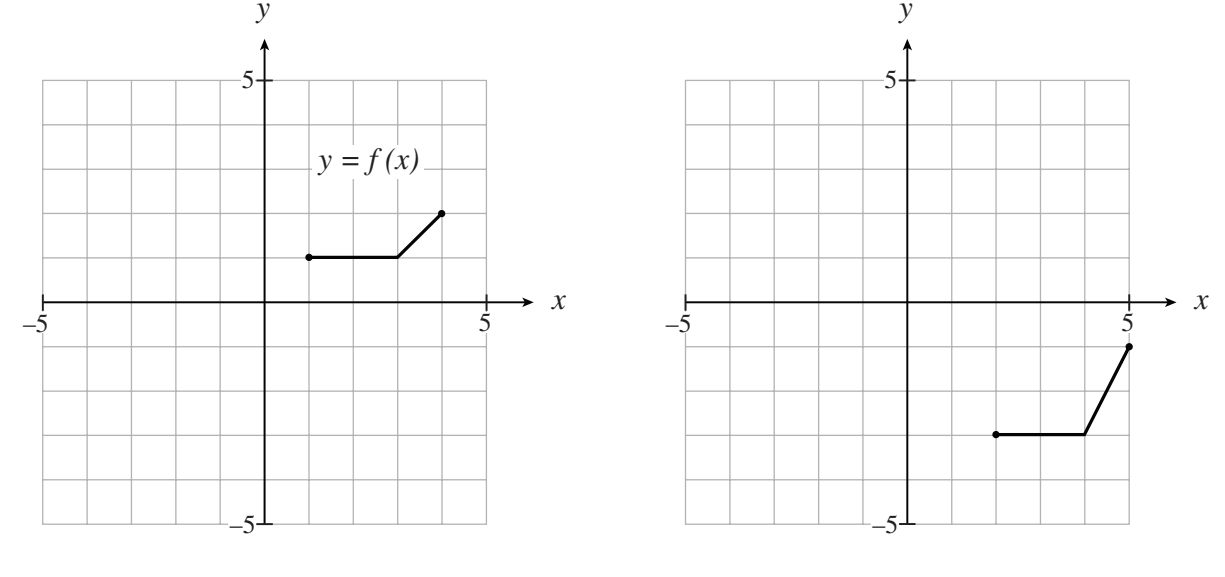
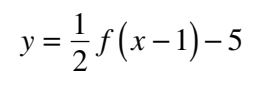 A
A 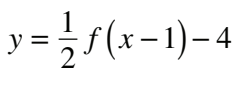 B
B 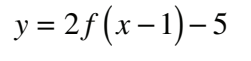 C
C 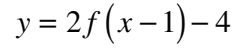 D
D 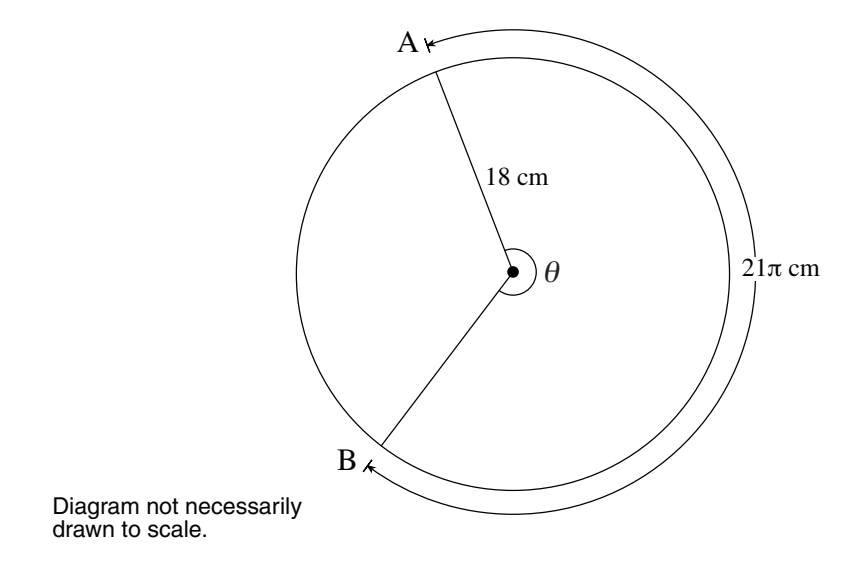
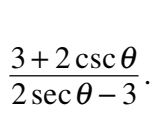
 A
A 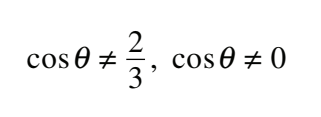 B
B 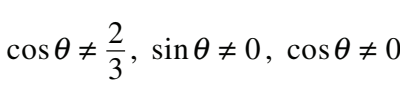 C
C  D
D 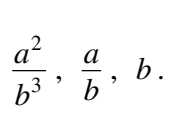
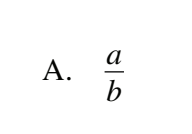 A
A 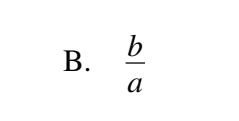 B
B 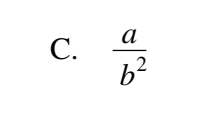 c
c 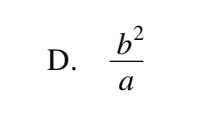 d
d